Im Kapitel Schleifen haben wir uns umständlich mit dem Berechnen der Fakultät beschäftigt. Hier ein kurzer Rückblick:
Die Fakultät von n ist dadurch definiert, dass alle Zahlen von 1 bis einschließlich n miteinander multipliziert werden:
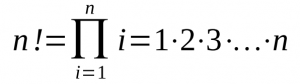
Um diese Fakultät zu berechnen müssen wird also alle Zahlen von 1 bis n multiplizieren. Das kann der Rechner jedoch nur Schrittweise, also:
1 ⋅ 2 = 2
2 ⋅ 3 = 6
6 ⋅ 4 = 24
24 ⋅ 5 = 120
⋮
Lesen wir die Rechnung von unten nach oben, dann fangen wir mit der Zahl an, von der wir die Fakultät berechnen wollen, und multiplizieren sie mit der Fakultät der nächst kleineren ganzen Zahl. Wir wollen also zum Beispiel die Fakultät von 5 berechnen, dann rechnen wir:
5 mal die Fakultät von 4: 5 ⋅ 24 = 5 ⋅ 4! = 120
4 mal die Fakultät von 3: 4 ⋅ 6 = 4 ⋅ 3! = 24
3 mal die Fakultät von 2: 3 ⋅ 2 = 3 ⋅ 2! = 6
2 mal die Fakultät von 1: 2 ⋅ 1 = 2 ⋅ 1! = 2
Fakultät von 1 ist nach Definition 1.
Das heißt wir können uns relativ einfach eine Funktion basteln, mit deren Hilfe wir die Fakultät berechnen und das komplett ohne eine Schleife zu bemühen. Dementsprechend müssen wir uns auch nicht darum kümmern, dass die Schleife ordentlich zählt.
Unser Ziel ist also folgende Funktion:
Fakultät(n) = n ⋅ Fakultät(n-1), unter der Voraussetzung, dass
Fakultät(1) = 1
Nichts leichter als das, wir kümmern uns ersteinmal um die Grundlage, dass die Fakultät der Zahl n immer dem Produkt aus der Zahl n und der Fakultät der Zahl n-1 entspricht und geben das als unser Ergebnis aus:
1
2
3
4
static Int64 fakultaet(Int64 n)
{
return n * fakultaet(n - 1);
}
Würden wir jetzt eine Fakultät berechnen wollen, dann würde unsere Funktion auch über 0 hinaus in den negativen Bereich rechnen und zwar prinzipiel unendlich lange. Da nicht mathematisierte Programmiersprachen den Wert unendlich nicht kennen, sondern immer Schranken für die Größe von Variablen besitzen, würden spätestens an der Schranke unsere Berechnungen falsch werden. C# erkennt, wenn Funktionen einander beziehungsweise sich selbst wiederholt aufrufen, ohne dass Werte zurückgegeben wurden. Ab einer bestimmten Anzahl solcher Aufrufe, die noch keinen Wert zurückgegeben haben, stoppt das Framework die Ausführung des Programm mit dem Fehler System.StackOverflowException. Das soll verhindern, dass der Arbeitsspeicher des Rechners bis an die Grenzen gefüllt wird und der Rechner nicht mehr reagieren kann. Sollte man über diesem Standardlimit arbeiten wollen, kann man das mit Hilfe der Variablen MAX_RECURSIVE_CALLS.
Aber zurück zu unserer Problemstellung. Wir wollen ja nicht bis minus Unendlich rechnen, sondern wir wissen, dass die Fakultät von 1 nach Definition 1 ist. Wir müssen jetzt also dafür sorgen, dass, sollte unsere Funktion die Fakultät von 1 berechnen, wir nicht wie sonst die nächst kleinere Fakultät berechnen, sondern den Wert 1 zurückgeben. Wir berechnen also die Fakultät wie bisher, für den Fall 1 geben wir aber den Wert 1 zurück:
1
2
3
4
5
6
7
static Int64 fakultaet(Int64 n)
{
if (n > 1)
return n * fakultaet(n - 1);
else
return 1;
}
Und schon sind wir fertig, wir können jetzt einfach die Funktion fakultaet(5); aufrufen, um die Fakultät von 5 zu berechnen und können diese dann zum Beispiel über ein Console.WriteLine(); ausgeben.
Diesen Prozess des sich immer selbst aufrufen, bis etwas bestimmtes eintritt nenn man Rekursion. Eine rekursive Funktion ruft sich also immer selbst wieder auf, bis ein vorher genau festgelegter Zustand eintritt. Diesen Zustand nennt man auch Abbruchzustand beziehungsweise Abbruchvorschrift/-bedingung. Jede rekursive Funktion muss mindestens eine dieser Abbruchbedingungen haben, da die Funktion sich sonst unendlich oft selbst aufruft, ohne dass diese jemals beendet werden würde.
Ein Schaudiagramm, welches die Rekurionstiefe verdeutlicht, sehen wir hier:
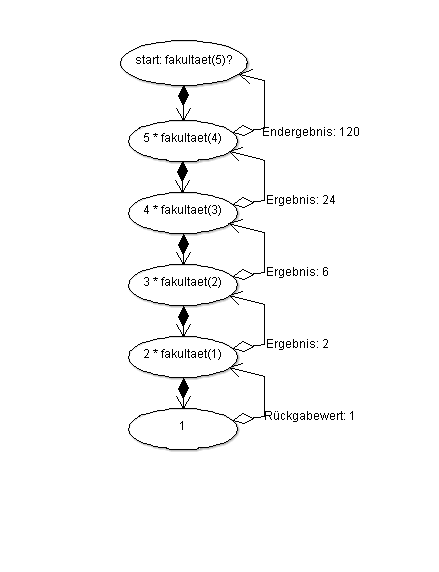
Wenn wir uns an die Bedingungen zurückerinnern, gab es auch eine Kurzschreibweise für simple Bedingungen. In Kurzschreibweise wird unsere Funktion zur Fakultätsberechnung sogar ein simpler Einzeiler:
1
2
3
4
static Int64 fakultaet_kurz(Int64 n)
{
return (n > 1) ? n * fakultaet_kurz(n - 1) : 1;
}